

The idea for communication without exchanging keys, came from my buddy Jeroen. In 2014 he told me how this can be achieved by combining two things:
There is a very old encryption technology called One-time pad (OTP). Since it uses a one-time key per message that is the same size or longer than the message, it cannot be cracked. OTP was first described in 1882 and in 1917, Gilbert Vernam used an XOR-operation to encrypt the message with a key. This algorithm is called the Vernam Cypher. As long as the key is truly random, cryptanalysis is impossible.
The vernam cypher is used to both encrypt and decrypt messages. Any encrypted message that is XOR-ed with a key, will result in the original message when it is XOR-ed with the same key again. Let me show you:
def xor(message, key):
return "".join([chr((ord(m) ^ ord(k))) for m, k in zip(message, key)])
message = "Hello"
key = "12345"
print(message) # show original message
encrypted = xor(message, key) # encrypt message
print(encrypted) # show encrypted message
decrypted = xor(encrypted, key) # decrypt message
print(decrypted) # show decrypted message
Output:
Hello
yW_XZ
Hello
This algorithm has an obvious weakness and that is that the keys need to be available to both the sender and the receiver of the messages. In the past, these keys had to be written down on a one-time pad and exchanged in a safe way. When exchanging new pads was not possible, or people were downright lazy, old pads were re-used. This allows for cryptanalysis. Would it be possible to encrypt messages without the sender and receiver having to exchange keys? Then Jeroen told me the story of the double bike-lock.
Hank wants to give his bike to Ingrid. Hank is available on monday and wednesday. Ingrid only on tuesday and thursday. They cannot meet in person. Here is a question for you: How can Hank park his bike in the city so it cannot be stolen, but Ingrid can take it?
The answer: Two locks.
On monday Hank parks his bike in the city and locks it with lock 1.
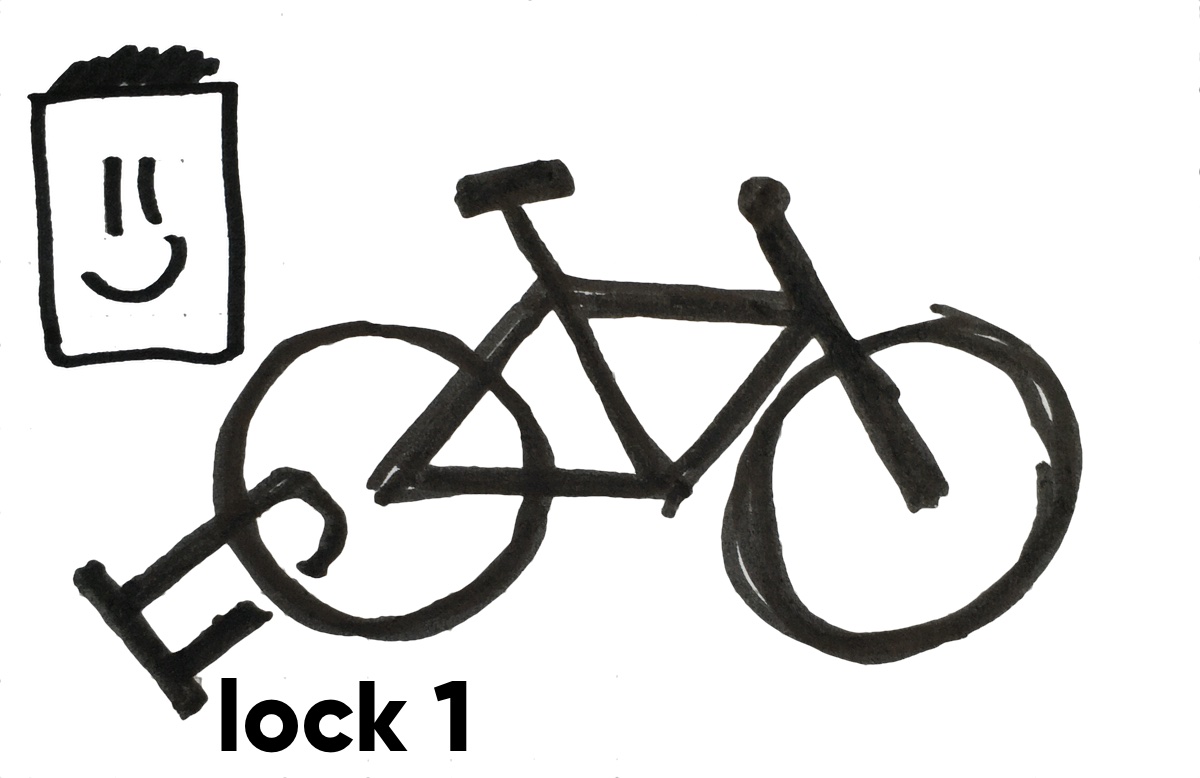
On tuesday Ingrid puts lock 2 on the bike. The bike is now secured with two locks.

On wednesday Hank comes back to the bike and removes lock 1.
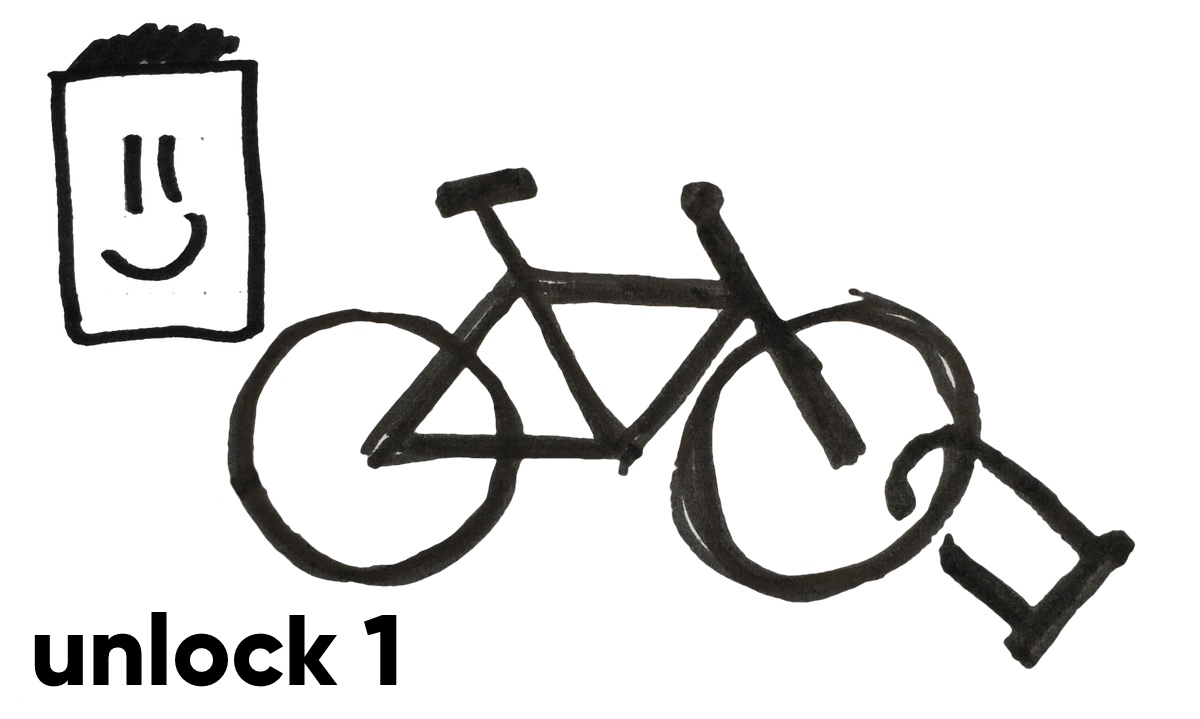
On thursday, Igrid removes lock 2. The bike is now unlocked and she can take the bike.

Notice that no keys or lock codes had to be exchanged. The only thing that Hank and Ingrid communicated is the location of the bike.
When Jeroen told me this story, it fascinated me. We asked ourselves the question: Does this work for encryption? Can Hank remove his encryption when the message is also encrypted with Ingrids key? The answer: Yes.
The XOR-operation allows this.
In the following python example, you see how a message is encrypted by Hank, then by Ingrid. Hank removes his encryption, then Ingrid removes her encryption. The result is the orginal message.
def xor(message, key):
return "".join([chr((ord(m) ^ ord(k))) for m, k in zip(message, key)])
message = "Hello"
key_hank = "12345"
key_ingrid = "54321"
print(message) # show original message
encrypted1 = xor(message, key_hank) # hank encrypts message
print(encrypted1) # show encrypted message
encrypted2 = xor(encrypted1, key_ingrid) # ingrid re-encrypts message
print(encrypted2) # show re-encrypted message
encrypted3 = xor(encrypted2, key_hank) # hank removes encryption
print(encrypted3) # show encrypted (only by ingrid) message
decrypted = xor(encrypted3, key_ingrid) # ingrid removes encryption
print(decrypted) # show decrypted message
Output:
Hello
yW_XZ
Lcljk
}Q_^^
Hello
Make sure the key is as long or longer than the message and it is a truly random value!
I am not a mathematician and certainly not a cryptography expert. I don’t know if this encryption method is safe of not. That said, I don’t see how it can be cracked. What am I missing here? If you know the answer, please send me a message. I would love to hear your thoughts.